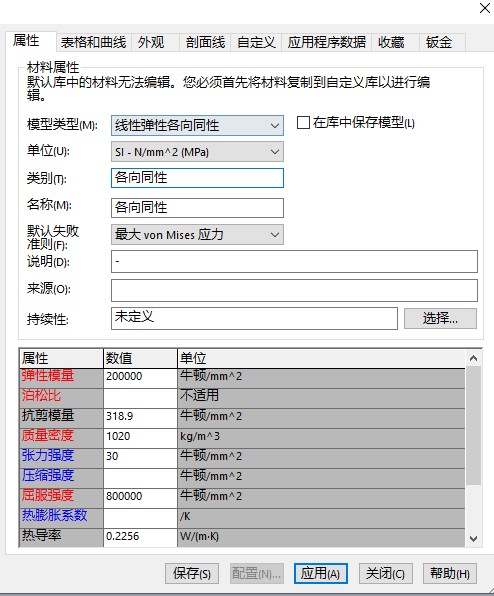

正应力是指物体在受力时,垂直于截面的应力。通过广义胡克定律推导得出,公式如下:
σₓ = (E / [(1 + ν)(1- 2ν)]) × [(1- ν)εₓ + ν(εᵧ + εz)]
σᵧ = (E / [(1 + ν)(1- 2ν)]) × [(1- ν)εᵧ + ν(εₓ + εz)]
σz = (E / [(1 + ν)(1- 2ν)]) × [(1- ν)εz + ν(εₓ + εᵧ)]
其中,E 为材料的弹性模量,ν 为泊松比,εₓ、εᵧ、εz 分别为 X、Y、Z 方向的正应变。
位移是指物体在受力后位置的改变。根据圣维南原理和相关边界条件,X,Y,Z方向的位移(u)计算公式为:
u = (F × L) / (E × A) + u₀
其中,L 为杆的长度,E泊松比,u₀ 为初始位移,(通常设为 0)。
公式计算结果:
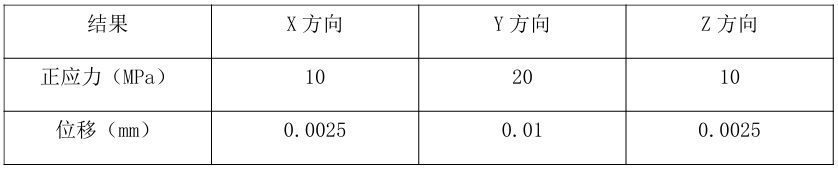
SOLIDWORKS Simulation 结果:
(1) X方向应力及位移结果:
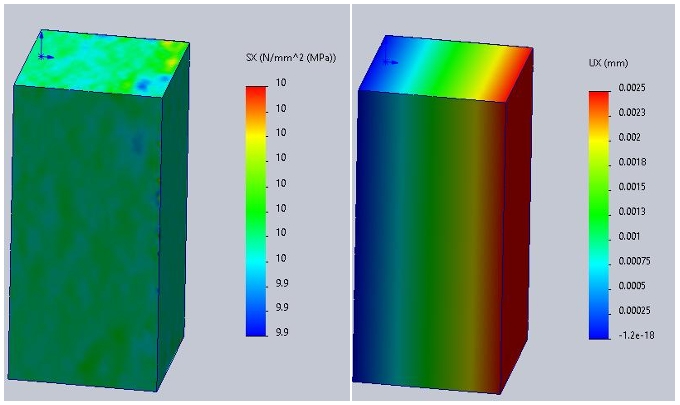
(2) Y方向应力及位移结果:

(3) Z方向应力及位移结果:
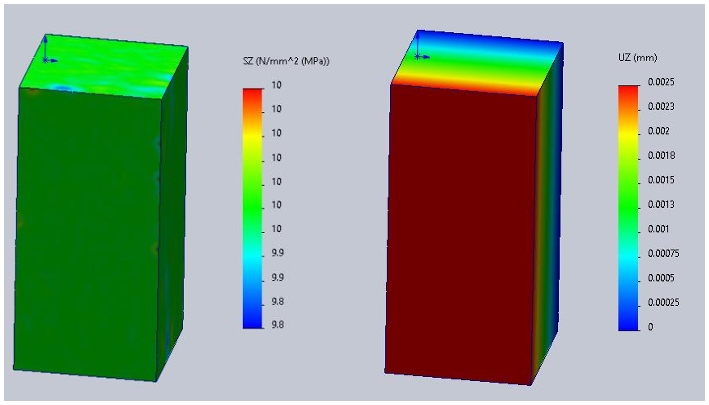
根据数据对比,公式计算与仿真结果一致,可以说明SOLIDWORKS Simulation的结果是可靠的。